Данная теорема устанавливает количественную взаимосвязь между работой силы (причиной) и кинетической энергией материальной точки (следствием).
Кинетической энергией материальной точки называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости
.
(43)
Кинетическая энергия характеризует то механическое действие силы, которое может превратиться в другие виды энергии, например, в тепловую.
Работой силы на данном перемещении называется характеристика того действия силы, которое приводит к изменению модуля скорости.
Элементарная работа силы определяется как скалярное произведение вектора силы на элементарный вектор перемещения в точке ее приложения
,
(44)
где
-
элементарное перемещение.
Модуль элементарной работы определяется формулой
где
- угол между вектором силы и вектором
элементарного перемещения;
-
проекция вектора силы на касательную.
Полная работа на некотором конечном перемещении определяется интегралом
.
(46)
Из (46) следует, что полная работа может быть вычислена в двух случаях, когда сила постоянная или зависит то перемещения.
При
F
=const
получаем
.
При решении задач часто удобно пользоваться аналитическим способом вычисления силы
где F x , F y , F z – проекции силы на координатные оси.
Докажем следующую теорему.
Теорема : Изменение кинетической энергии материальной точки на некотором ее перемещении равно работе силы, действующей на точку, на том же перемещении.
Пусть материальная точка M массы m движется под действием силы F из положения M 0 в положение M 1 .
ОУД:
.
(47)
Введем
подстановку
и спроектируем (47)
на касательную
.
(48)
Разделяем в (48) переменные и интегрируем
В результате получим
.
(49)
Уравнение (49) доказывает сформулированную выше теорему.
Теоремой удобно пользоваться, когда среди заданных и искомых параметров присутствуют масса точки, ее начальная и конечная скорость, силы и перемещение.
Вычисление работы характерных сил.
1. Работа силы тяжести вычисляется как произведение модуля силы на перемещение точки ее приложения по вертикали
.
(50)
При перемещении вверх работа положительная, при перемещении вниз – отрицательная.
2. Работа упругой силы пружины F =-cx равна
,
(51)
где x 0 – начальное удлинение (сжатие) пружины;
x 1 – конечное удлинение (сжатие) пружины.
Работа силы тяжести и упругой силы не зависят от траектории перемещения их точек приложения. Такие силы, работа которых не зависит от траектории, называются потенциальными силами .
3. Работа силы трения .
Так как сила трения всегда направлена в сторону, противоположную направлению перемещения, то ее работа равна
Работа силы трения всегда отрицательная . Силы работа которых всегда отрицательна, называются диссипативными .
Кинетическая энергия механической системы складывается из кинетических энергий всех её точек:
Дифференцируя каждую часть этого равенства по времени, получим
Воспользовавшись основным законом динамики для к -й точки системы m k 2i k = Fj., приходим к равенству
Скалярное произведение силы F на скорость v точки её приложения называют мощностью силы и обозначают Р :
Используя это новое обозначение, представим (11.6) в следующем виде:
Полученное равенство выражает дифференциальную форму теоремы об изменении кинетической энергии: скорость изменения кинетической энергии механической системы равна сумме jмощностей всех действующих на систему cm.
Предс тавив производную f в (8.5) в форме дроби -- и выполнив
затем разделение переменных, получим:
где dT - дифференциал кинетической энергии, т.е. её изменение за бесконечно малый промежуток времени dr, dr k = k dt - элементарное перемещение к- й точки системы, т.е. перемещение за время dt.
Скалярное произведение силы F на элементарное перемещение dr точки её приложения называют элементарной работой силы и обозначают dA:
Используя свойства скалярного произведения можно представить элементарную работу силы также в виде
Здесь ds = dr - длина дуги траектории точки приложения силы, соответствующая её элементарному перемещению с/г; а - угол между направлениями вектора силы F и вектора элементарного перемещения c/r; F„ F y , F, - проекции вектора силы F на декартовы оси; dx, dy, dz - проекции на декартовы оси вектора элементарного перемещения с/г.
С учетом обозначения (11.9) равенство (11.8) можно представить в следующей форме:
т.е. дифференциал кинетической энергии системы равен сумме элементарных работ всех сил, действующих на систему. Это равенство, так же как и (11.7), выражает дифференциальную форму теоремы об изменении кинетической энергии, но отличается от (11.7) тем, что использует не производные, а бесконечно малые приращения - дифференциалы.
Выполняя почленное интегрирование равенства (11.12), получаем
где в качестве пределов интегрирования использованы: 7 0 - кинетическая энергия системы в момент времени? 0 ; 7) - кинетическая энергия системы в момент времени t x .
Определенные интегралы по временному отрезку или A(F):
Замечание 1. Для вычисления работы иногда удобнее использовать не дуговую параметризацию траектории M(s), а координатную M(x{t), у(/), z(f)). В этом случае для элементарной работы естественно взять представление (11.11), а криволинейный интеграл представить в виде:
С учетом обозначения (11.14) работы на конечном перемещении равенство (11.13) принимает вид
и представляет собой конечную форму теоремы об изменении кинетической энергии механической системы.
Теорема 3. Изменение кинетической энергии механической системы при её перемещении из начального положения в конечное равно сумме работ всех сил, действующих на точки системы на этом перемещении.
Замечание
2. В правой части равенства (11.16) учитываются работы всех сил
, действующих на систему, как внешних, так и внутренних. Тем не менее существуют такие механические системы, для которых суммарная работа всех внутренних сил равна нулю. Эго гак называемые неизменяемые системы
, у которых расстояния между взаимодействующими материальными точками не меняются. Например, система твердых тел, связанных шарнирами без трения или гибкими нерастяжимыми нитями. Для таких систем в равенстве (11.16) достаточно учесть лишь работы внешних сил, т.е. теорема (11.16) принимает вид:
Энергией называется скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие.
Для характеристики различных форм движения материи вводятся соответствующие виды энергии, например: механическая, внутренняя, энергия электростатических, внутриядерных взаимодействий и др.
Энергия подчиняется закону сохранения, который является одним из важнейших законов природы.
Механическая энергия Е характеризует движение и взаимодействие тел и является функцией скоростей и взаимного расположения тел. Она равна сумме кинетической и потенциальной энергий.
Кинетическая энергия
Рассмотрим случай, когда на тело массой m действует постоянная сила \(~\vec F\) (она может быть равнодействующей нескольких сил) и векторы силы \(~\vec F\) и перемещения \(~\vec s\) направлены вдоль одной прямой в одну сторону. В этом случае работу силы можно определить как A = F ∙s . Модуль силы по второму закону Ньютона равен F = m∙a , а модуль перемещения s при равноускоренном прямолинейном движении связан с модулями начальной υ 1 и конечной υ 2 скорости и ускорения а выражением \(~s = \frac{\upsilon^2_2 - \upsilon^2_1}{2a}\) .
Отсюда для работы получаем
\(~A = F \cdot s = m \cdot a \cdot \frac{\upsilon^2_2 - \upsilon^2_1}{2a} = \frac{m \cdot \upsilon^2_2}{2} - \frac{m \cdot \upsilon^2_1}{2}\) . (1)
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела .
Кинетическая энергия обозначается буквой E k .
\(~E_k = \frac{m \cdot \upsilon^2}{2}\) . (2)
Тогда равенство (1) можно записать в таком виде:
\(~A = E_{k2} - E_{k1}\) . (3)
Теорема о кинетической энергии
работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.
Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.
Если начальная скорость движения тела массой m равна нулю и тело увеличивает свою скорость до значения υ , то работа силы равна конечному значению кинетической энергии тела:
\(~A = E_{k2} - E_{k1}= \frac{m \cdot \upsilon^2}{2} - 0 = \frac{m \cdot \upsilon^2}{2}\) . (4)
Физический смысл кинетической энергии
кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.
Потенциальная энергия
Потенциальная энергия – это энергия взаимодействия тел.
Потенциальная энергия поднятого над Землей тела – это энергия взаимодействия тела и Земли гравитационными силами. Потенциальная энергия упруго деформированного тела – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Потенциальными называются силы , работа которых зависит только от начального и конечного положения движущейся материальной точки или тела и не зависит от формы траектории.
При замкнутой траектории работа потенциальной силы всегда равна нулю. К потенциальным силам относятся силы тяготения, силы упругости, электростатические силы и некоторые другие.
Силы , работа которых зависит от формы траектории, называются непотенциальными . При перемещении материальной точки или тела по замкнутой траектории работа непотенциальной силы не равна нулю.
Потенциальная энергия взаимодействия тела с Землей
Найдем работу, совершаемую силой тяжести F т при перемещении тела массой m вертикально вниз с высоты h 1 над поверхностью Земли до высоты h 2 (рис. 1). Если разность h 1 – h 2 пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяжести F т во время движения тела можно считать постоянной и равной mg .
Так как перемещение совпадает по направлению с вектором силы тяжести, работа силы тяжести равна
\(~A = F \cdot s = m \cdot g \cdot (h_1 - h_2)\) . (5)
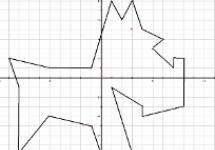
Рассмотрим теперь движение тела по наклонной плоскости. При перемещении тела вниз по наклонной плоскости (рис. 2) сила тяжести F т = m∙g совершает работу
\(~A = m \cdot g \cdot s \cdot \cos \alpha = m \cdot g \cdot h\) , (6)
где h – высота наклонной плоскости, s – модуль перемещения, равный длине наклонной плоскости.
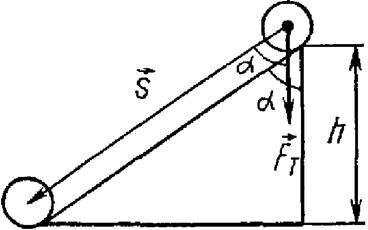
Движение тела из точки В в точку С по любой траектории (рис. 3) можно мысленно представить состоящим из перемещений по участкам наклонных плоскостей с различными высотами h ’, h ’’ и т. д. Работа А силы тяжести на всем пути из В в С равна сумме работ на отдельных участках пути:
\(~A = m \cdot g \cdot h" + m \cdot g \cdot h"" + \ldots + m \cdot g \cdot h^n = m \cdot g \cdot (h" + h"" + \ldots + h^n) = m \cdot g \cdot (h_1 - h_2)\) , (7)
где h 1 и h 2 – высоты от поверхности Земли, на которых расположены соответственно точки В и С .
Равенство (7) показывает, что работа силы тяжести не зависит от траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях.
При движении вниз работа силы тяжести положительна, при движении вверх – отрицательна. Работа силы тяжести на замкнутой траектории равна нулю.
Равенство (7) можно представить в таком виде:
\(~A = - (m \cdot g \cdot h_2 - m \cdot g \cdot h_1)\) . (8)
Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.
Работа силы тяжести при перемещении тела массой m из точки, расположенной на высоте h 2 , в точку, расположенную на высоте h 1 от поверхности Земли, по любой траектории равна изменению потенциальной энергии взаимодействия тела и Земли, взятому с противоположным знаком.
\(~A = - (E_{p2} - E_{p1})\) . (9)
Потенциальная энергия обозначается буквой Е p .
Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, т. е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.
При таком выборе нулевого уровня потенциальная энергия Е p тела, находящегося на высоте h над поверхностью Земли, равна произведению массы m тела на модуль ускорения свободного падения g и расстояние h его от поверхности Земли:
\(~E_p = m \cdot g \cdot h\) . (10)
Физический смысл потенциальной энергии взаимодействия тела с Землей
потенциальная энергия тела, на которое действует сила тяжести, равна работе, совершаемой силой тяжести при перемещении тела на нулевой уровень.
В отличие от кинетической энергии поступательного движения, которая может иметь лишь положительные значения, потенциальная энергия тела может быть как положительной, так и отрицательной. Тело массой m , находящееся на высоте h , где h < h 0 (h 0 – нулевая высота), обладает отрицательной потенциальной энергией:
\(~E_p = -m \cdot g \cdot h\) .
Потенциальная энергия гравитационного взаимодействия
Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами m и М , находящихся на расстоянии r одна от другой, равна
\(~E_p = G \cdot \frac{M \cdot m}{r}\) . (11)
где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е p = 0) принят при r = ∞.
Потенциальная энергия гравитационного взаимодействия тела массой m с Землей, где h – высота тела над поверхностью Земли, M e – масса Земли, R e – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.
\(~E_e = G \cdot \frac{M_e \cdot m \cdot h}{R_e \cdot (R_e +h)}\) . (12)
При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой m с Землей для малых высот h (h « R e) равна
\(~E_p = m \cdot g \cdot h\) ,
где \(~g = G \cdot \frac{M_e}{R^2_e}\) – модуль ускорения свободного падения вблизи поверхности Земли.
Потенциальная энергия упруго деформированного тела
Вычислим работу, совершаемую силой упругости при изменении деформации (удлинения) пружины от некоторого начального значения x 1 до конечного значения x 2 (рис. 4, б, в).
Сила упругости изменяется в процессе деформации пружины. Для нахождения работы силы упругости можно взять среднее значение модуля силы (т.к. сила упругости линейно зависит от x ) и умножить на модуль перемещения:
\(~A = F_{upr-cp} \cdot (x_1 - x_2)\) , (13)
где \(~F_{upr-cp} = k \cdot \frac{x_1 - x_2}{2}\) . Отсюда
\(~A = k \cdot \frac{x_1 - x_2}{2} \cdot (x_1 - x_2) = k \cdot \frac{x^2_1 - x^2_2}{2}\) или \(~A = -\left(\frac{k \cdot x^2_2}{2} - \frac{k \cdot x^2_1}{2} \right)\) . (14)
Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:
\(~E_p = \frac{k \cdot x^2}{2}\) . (15)
Из формул (14) и (15) следует, что работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому с противоположным знаком:
\(~A = -(E_{p2} - E_{p1})\) . (16)
Если x 2 = 0 и x 1 = х , то, как видно из формул (14) и (15),
\(~E_p = A\) .
Физический смысл потенциальной энергии деформированного тела
потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Потенциальная энергия характеризует взаимодействующие тела, а кинетическая энергия – движущиеся тела. И потенциальная, и кинетическая энергия изменяются только в результате такого взаимодействия тел, при котором действующие на тела силы совершают работу, отличную от нуля. Рассмотрим вопрос об изменениях энергии при взаимодействиях тел, образующих замкнутую систему.
Замкнутая система – это система, на которую не действуют внешние силы или действие этих сил скомпенсировано . Если несколько тел взаимодействуют между собой только силами тяготения и силами упругости и никакие внешние силы на них не действуют, то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии тел, взятому с противоположным знаком:
\(~A = -(E_{p2} - E_{p1})\) . (17)
По теореме о кинетической энергии, работа тех же сил равна изменению кинетической энергии:
\(~A = E_{k2} - E_{k1}\) . (18)
Из сравнения равенств (17) и (18) видно, что изменение кинетической энергии тел в замкнутой системе равно по абсолютному значению изменению потенциальной энергии системы тел и противоположно ему по знаку:
\(~E_{k2} - E_{k1} = -(E_{p2} - E_{p1})\) или \(~E_{k1} + E_{p1} = E_{k2} + E_{p2}\) . (19)
Закон сохранения энергии в механических процессах :
сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и си-лами упругости, остается постоянной.
Сумма кинетической и потенциальной энергии тел называется полной механической энергией .
Приведем простейший опыт. Подбросим вверх стальной шарик. Сообщив начальную скорость υ нач, мы придадим ему кинетическую энергию, из-за чего он начнет подниматься вверх. Действие силы тяжести приводит к уменьшению скорости шарика, а значит, и его кинетической энергии. Но шарик поднимается выше и выше и приобретает все больше и больше потенциальной энергии (Е p = m∙g∙h ). Таким образом, кинетическая энергия не исчезает бесследно, а происходит ее превращение в потенциальную энергию.
В момент достижения верхней точки траектории (υ = 0) шарик полностью лишается кинетической энергии (Е k = 0), но при этом его потенциальная энергия становится максимальной. Дальше шарик меняет направление движения и с увеличивающейся скоростью движется вниз. Теперь происходит обратное превращение потенциальной энергии в кинетическую.
Закон сохранения энергии раскрывает физический смысл понятия работы :
работа сил тяготения и сил упругости, с одной стороны, равна увеличению кинетической энергии, а с другой стороны, – уменьшению потенциальной энергии тел. Следовательно, работа равна энергии, превратившейся из одного вида в другой.
Закон об изменении механической энергии
Если система взаимодействующих тел не замкнута, то ее механическая энергия не сохраняется. Изменение механической энергии такой системы равно работе внешних сил:
\(~A_{vn} = \Delta E = E - E_0\) . (20)
где Е и Е 0 – полные механические энергии системы в конечном и начальном состояниях соответственно.
Примером такой системы может служить система, в которой наряду с потенциальными силами действуют непотенциальные силы. К непотенциальным силам относятся силы трения. В большинстве случаев, когда угол между силой трения F r тела составляет π радиан, работа силы трения отрицательна и равна
\(~A_{tr} = -F_{tr} \cdot s_{12}\) ,
где s 12 – путь тела между точками 1 и 2.
Силы трения при движении системы уменьшают ее кинетическую энергию. В результате этого механическая энергия замкнутой неконсервативной системы всегда уменьшается, переходя в энергию немеханических форм движения.
Например, автомобиль, двигавшийся по горизонтальному участку дороги, после выключения двигателя проходит некоторый путь и под действием сил трения останавливается. Кинетическая энергия поступательного движения автомобиля стала равной нулю, а потенциальная энергия не увеличилась. Во время торможения автомобиля произошло нагревание тормозных колодок, шин автомобиля и асфальта. Следовательно, в результате действия сил трения кинетическая энергия автомобиля не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.
Закон сохранения и превращения энергии
при любых физических взаимодействиях энергия превращается из одной формы в другую.
Иногда угол между силой трения F tr и элементарным перемещением Δr равен нулю и работа силы трения положительна:
\(~A_{tr} = F_{tr} \cdot s_{12}\) ,
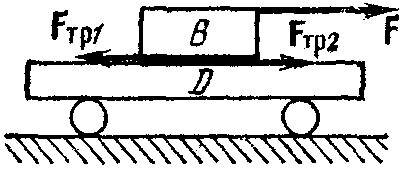
Пример 1 . Пусть, внешняя сила F действует на брусок В , который может скользить по тележке D (рис. 5). Если тележка перемещается вправо, то работа силы трения скольжения F tr2 , действующей на тележку со стороны бруска, положительна:
Пример 2 . При качении колеса его сила трения качения направлена вдоль движения, так как точка соприкосновения колеса с горизонтальной поверхностью двигается в направлении, противоположном направлению движения колеса, и работа силы трения положительна (рис. 6):
Литература
- Кабардин О.Ф. Физика: Справ. материалы: Учеб. пособие для учащихся. – М.: Просвещение, 1991. – 367 с.
- Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. сред. шк. – М.: Про-свещение, 1992. – 191 с.
- Элементарный учебник физики: Учеб. пособие. В 3 т. / Под ред. Г.С. Ландсберга: т. 1. Механика. Теплота. Молекулярная физика. – М.: Физматлит, 2004. – 608 с.
- Яворский Б.М., Селезнев Ю.А. Справочное руководство по физике для поступающих в вузы и самообразования. – М.: Наука, 1983. – 383 с.
Кинетической энергией материальной точки k называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости . Кинетической энергией механической системы называется арифметическая сумма кинетических энергий всех точек системы
. (3.35)
Найдем формулы для вычисления кинетической энергии тел в разных случаях движения.
Поступательное движение . В этом случае скорости всех точек тела одинаковы , где скорость центра масс тела.
Вращательное движение . Скорость –ой точки тела , где расстояние точки до оси вращения.
, (3.37)
где момент инерции тела относительно оси вращения .
Плоское движение . Из кинематики известно, что плоское движение в некоторый момент времени можно рассматривать как мгновенный поворот тела вокруг оси, проходящей через мгновенный центр скоростей.
В этом случае . Пусть точка – центр масс. По теореме Гюйгенса-Штейнера (3.22): 
. Кинетическая энергия тела при плоском движении
. (3.38)
Здесь момент инерции тела относительно центральной оси, скорость центра масс, мгновенная угловая скорость, – масса тела.
Докажем теорему об изменении кинетической энергии для материальной точки . Запишем второй закон Ньютона в проекции на касательную (3.5): .
Касательное ускорение
. Следовательно, закон Ньютона примет вид
или 
, (3.39)
где элементарная работа силы на перемещении точки . Элементарную работу можно записать иначе:
· . (3.40)
Здесь · скалярное произведение векторов, 
радиус-вектор точки .
Поскольку , то аналитическое выражение элементарной работы силы :
Проинтегрировав (3.39) в пределах изменения переменных в точках и , найдем окончательно
. (3.42)
Это уравнение выражает теорему об изменении кинетической энергии материальной точки в интегральной форме: изменение кинетической энергии точки на некотором ее перемещении равно сумме работ приложенных сил на том же перемещении.
Для произвольной точки механической системы выражение(3.42) имеет вид: 
. Для всей системы 
. Если обозначить кинетическую энергию всей системы в ее начальном положении
А в конечном положении , то
. (3.43)
Уравнение (3.43) выражает теорему об изменении кинетической энергии механической системы в интегральной форме: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил. Отметим, что в общем случае сумма работ внутренних сил не равна нулю. Для абсолютно твердого тела , так как расстояния между любыми точками тела не изменяются.
Работа силы тяжести
. Пусть точка переместилась под действием силы тяжести из положения в положение (рис. 3.7). По формуле (3.41) найдем элементарную работу силы : Полная работа силы на перемещении будет 
или
 |
где − высота, на которую опустилась точка. Таким образом, работа силы тяжести положительна, когда точка опускается, и отрицательна, когда точка поднимается.
Работа силы упругости пружины
. Пусть груз прикреплен к пружине жесткости с
(рис. 3.8). Выберем начало координаты в положении , при котором пружина не деформирована (ее длина равна l
), и определим работу силы упругости пружины при перемещении ее нижнего конца из начального положения в конечное положение . Пусть λ , λ начальная и конечная деформации пружины. Согласно закону Гука . Проекции силы на оси координат: . Элементарная работа 
. Полная работа
– λ –λ )или = (λ –λ ). (3.45)
Работа силы упругости положительна, если начальная λ деформация пружины больше конечной λ .
Работа силы трения скольжения . Пусть тело перемещается по наклонной шероховатой плоскости из положения в положение . Действующая на тело сила трения , где – нормальная реакция плоскости, – коэффициент трения скольжения. Сила трения направлена противоположно перемещению тела, поэтому работа силы трения отрицательна. Если считать силу трения во время движения постоянной, то. Нетрудно заметить, что – момент силы относительно оси вращения . Будем называть величину вращающим моментом . Тогда элементарная работа . При повороте на конечный угол работа
, (3.47)
а в случае постоянного момента из (3.47) следует .
Вопросы для самоконтроля
механической системы
Кинетической энергией механической системы называется арифметическая сумма кинетических энергий всех ее материальных точек
Вычисление кинетической энергии твердого тела
1. Поступательное движение
Как известно, при поступательном движении скорости всех точек тела в один и тот же момент времени равны, тогда (83) можно представить в виде
.
(84)
При поступательном движении тела, его кинетическая энергия равна половине произведения массы на квадрат скорости центра масс.
2. Вращательное движение твердого тела
П
ри
вращательном движении скорость каждой
точки тела
.
(85)
Подставим (85) в (83):
.
Принимая во внимание (59), получим
.
(86)
При вращательном движении кинетическая энергия равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости.
3 . Плоское движение
Плоское движение можно представить как вращение относительно полюса (например, центра масс) и движения вместе с полюсом, тогда
.
(87)
Кинетическая энергия тела при плоском движении равна сумме кинетических энергий от поступательного движения вместе с центром масс и вращательного движения относительно центра масс.
Теорема: Изменение кинетической энергии механической системы на некотором ее перемещении равно сумме работ всех внутренних и внешних сил системы на том же перемещении
.
(88)
Замечания :
1. Введенная величина кинетической энергии системы в отличие от количества движения системы и кинетического момента является скалярной величиной. При этом:
Q =0 при вращательном движении и покое;
K O =0 при поступательном движении или покое;
T
Таким образом, в отличие от теоремы об изменении количества движения и кинетического момента, данная теорема пригодна для изучения любого вида движения, так как T =0 только для неподвижной системы.
2. В отличие от упомянутых теорем данная теорема учитывает действие внутренних сил системы.
Некоторые случаи вычисления работы
1. Работа момента силы M Z относительно оси равна произведению момента на угол поворота тела относительно оси
.
(89)
2. Сумма работ внутренних сил абсолютно твердого тела (недеформируемого) всегда равна нулю.
3.
Работа
момента трения качения
.
,
где - коэффициент трения качения;
R – радиус цилиндра;
s – длина дуги, равная отрезку пути, пройденного центром масс C вдоль поверхности;
-
угол поворота осей цилиндра в процессе
движения;
N – нормальная реакция поверхности;
P – сила тяжести;
F тр – сила трения скольжения.
Дифференциальные уравнения поступательного, вращательного и плоского движения твердого тела
1. Поступательное движение
При поступательном движении все точки тела движутся по одинаковым траекториям и в один и тот же момент времени имеют одинаковые ускорения. Тогда для описания движения можно использовать теорему о движении центра масс (67). Проектируем это уравнение на координатные оси
Система (90) представляет собой дифференциальные уравнения поступательного движения твердого тела.
2. Вращательное движение
П
усть
твердое тело совершает вращение
относительно оси под действием сил.
Динамической характеристикой
вращательного движения твердого тела
является кинетический моментK
z
,
а характеристикой вращательного
действия силы
момент силы относительно оси. Поэтому
для описания вращательного движения
твердого тела относительно неподвижной
оси воспользуемся теоремой об изменении
кинетического момента (81)
.
(91)
При
вращательном движении
,
тогда
,
учитывая, что I z =const, в итоге получим
.
(92)
Уравнение (92) представляет собой дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.
Найденный угол будет определять положение тела, совершающего вращательное движение, в любой момент времени.
3. Плоское движение
Положение тела, совершающего плоское движение, в любой момент времени определяется положением полюса и углом поворота тела относительно полюса. Если за полюс принять центр масс тела, то уравнение его движения можно найти по теореме о движении центра масс (67), а вращательное движение относительно центра будет определяться уравнением (92), справедливым и для движения системы относительно оси, проходящей через центр масс. Тогда дифференциальные уравнения плоского движения твердого тела имеют вид
