Вычисление площади фигуры.

Метод Пика

Работа обучающейся 5Б класса МБОУ СОШ №23 г. Иркутска

Балсуковой Александры

Руководитель: Ходырева Т.Г.

2014г.

Вычисление площади фигуры. Метод Пика

Объект исследования : задачи на клетчатой бумаге

Предмет исследования : задач на вычисление площади многоугольника на клетчатой бумаге, методы и приёмы их решения.

Методы исследования : сравнение, обобщение, аналогии, изучение литературы и Интернет-ресурсов, анализ информации.

Цель исследования:

выбрать главную, интересную, понятную информацию

Проанализировать и систематизировать полученную информацию

Найти различные методы и приёмы решения задач на клетчатой бумаге

проверить формулы вычисления площадей геометрических фигур с помощью формулы Пика

Создать электронную презентацию работы для представления собранного материала

Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать.

(Г. Галилей)

Актуальность темы

Увлечение математикой часто начинается с размышления над какой-то задачей. Так при изучении темы «Площади многоугольников» встает вопрос есть ли задачи, отличные от задач рассмотренных в учебнике. К таким задачам можно отнести задачи на клетчатой бумаге. В чём заключается особенность таких задач, существуют ли специальные методы и приёмы решения задач на клетчатой бумаге. На уроке математики учитель познакомила нас с интересным методом вычисления многоугольников. Я приступила к изучению литературы, Интернет-ресурсов по данной теме. Казалось бы, что увлекательного можно найти на клетчатой плоскости, то есть, на бесконечном листке бумаги, расчерченном на одинаковые квадратики. Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны. Я научилась вычислять площади многоугольников, нарисованных на клетчатом листке. Для многих задач на бумаге в клетку нет общего правила решения, конкретных способов и приёмов. Вот это их свойство обуславливает их ценность для развития не конкретного учебного умения или навыка, а вообще умения думать, размышлять, анализировать, искать аналогии, то есть, эти задачи развивают мыслительные навыки в самом широком их понимании.

И еще я узнала, что такие задачи рассматриваются в контрольно – измерительных материалах ГИА и ЕГЭ. Поэтому, считаю изучение этого материала полезным для применения его не только в дальнейшем учебном процессе, но и для решения нестандартных олимпиадных задач.

2.Понятие площади

Площадь - численная характеристика двумерной геометрической фигуры, показывающая размер этой фигуры. Исторически вычисление площади называлось . Фигура, имеющая площадь, называется квадрируемой .

Площадь плоской фигуры с точки зрения геометрии

1. Площадь -мера плоской фигуры по отношению к стандартной фигуре, являющейся квадратом со стороной, равной единице длины.

2. Площадь - численная характеристика, приписываемая плоским фигурам определенного класса (например, многоугольникам). Площадь квадрата со стороной, равной единице длины, принимаемая равной единице площади

3. Площадь - положительная величина, численное значение которой обладает следующими свойствами:

 Равные фигуры имеют равные площади;

 Если фигура разбивается на части, являющиеся простыми фигурами (т.е. те, которые можно разбить на конечное число плоских треугольников), то площадь этой фигуры равна сумме площадей ее частей;

 Площадь квадрата со стороной, равной единице измерения, равна единице.

Таким образом, можно сделать вывод, что площадь не является конкретной величиной, а только дает некоторую условную характеристику какой-либо плоской фигуры. Чтобы найти площадь произвольной фигуры, то необходимо определить, сколько квадратов со стороной, равной единице длины, она в себя вмещает. Например, возьмем прямоугольник, в котором квадратный сантиметр укладывается ровно 6 раз. Это означает, что площадь прямоугольника равняется 6 см 2 .

Выбор площади квадрата со стороной, равной единице измерения, в качестве минимальной единицы измерения всех площадей не случаен. Это результат договоренности между людьми, возникший в ходе «естественного» многовекового отбора. Кроме того, были и другие предложения о единице измерения. Так, например, за такую единицу предлагалось взять площадь равностороннего треугольника (т.е. любую плоскую фигуру можно было представить в виде «суммы» некоего числа равносторонних треугольников), что привело бы к изменению численного представления площадей.

Таким образом, формулы для вычисления площадей появились в математике и осознались человеком не сразу-это многих ученых, проживающих в разные эпохи и разных странах. (Ошибочные формулы не находили место в науке и уходили в небытие). Истинные же формулы дополнялись, исправлялись и обосновывались на протяжений тысячелетий, пока не дошли до нас в их современном обличии.

Само же измерение площади состоит в сравнении площади данной фигуры с площадью фигуры, принятой за единицу измерения. В результате сравнения получается некоторое число- численное значение площади данной фигуры. Это число показывает, во сколько раз площадь данной фигуры больше (или меньше) площади фигуры, принятой за единицу измерения площади.

Таким образом, можно сделать вывод, что площадь-это искусственная величина, исторически введенная человеком для измерения некоторого свойства плоской фигуры. Необходимость ввода такой величины обуславливалась возрастающими потребностями в знании того, насколько большая та или иная территория, сколько надо зерна, чтобы засеять поле или вычислить площадь поверхности пола для украшения орнаментной плитки.

Формула Пика

Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Точнее, если S – площадь многоугольника, В - число клеток, которые целиком лежат внутри многоугольника, и Г - число клеток, которые имеют с внутренностью. Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги – в таких, где пересекаются линии сетки многоугольника хоть одну общую точку.

Площадь любого треугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим через вершины нарисованного треугольника.

Для вычисления площади такого многоугольника можно воспользоваться следующей теоремой:

Теорема . Пусть - число целочисленных точек внутри многоугольника, - количество целочисленных точек на его границе, - его площадь. Тогда справедлива формула Пика :

Пример. Для многоугольника на рисунке L = 7 (красные точки), 9 (зеленые точки), поэтому S = 7+ 9/2 -1 = 10,5 квадратных единиц.

Теорема Пика - классический результат и .

Площадь треугольника с вершинами в узлах и не содержащего узлов ни внутри, ни на сторонах (кроме вершин), равна 1/2. Этот факт.

3. История

Формула Пика была открыта австрийским математиком Георгом Александром (1859-1942) в г.. В 16 лет Георг закончил школу и поступил в . В 20 лет получил право преподавать физику и математику. В 1884 году Пик уехал в к . Там он познакомился с другим учеником Клейна, . Позже, в 1885 году, он вернулся в , где и прошла оставшаяся часть его научной карьеры.

Георг Пик дружил с Эйнштейном. Пик и Эйнштейн не только имели общие научные интересы, но и страстно увлекались музыкой. Пик, игравший в квартете, который состоял из университетских профессоров, ввёл Эйнштейна в научное и музыкальное общества Праги.

Круг математических интересов Пика был чрезвычайно широк. В частности, им более 50 научных работ. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники.

4.Приложения формулы Пика

Формула Пика используется не только для вычисления площадей многоугольников, но и для решения многих задач олимпиадного уровня.

Некоторые примеры использования формулы Пика при решении задач:

1) Шахматный король обошел доску 8 × 8 клеток, побывав на каж-

дом поле ровно один раз и последним ходом вернувшись на исходное

поле. Ломаная, соединяющая последовательно центры полей, которые

проходил король, не имеет самопересечений. Какую площадь может

ограничивать эта ломаная? (Сторона клетки равна 1.)

Из формулы Пика сразу следует, что площадь, ограниченная ло-

маной, равна 64/2 − 1 = 31; здесь узлами решетки служат центры 64

полей и, по условию, все они лежат на границе многоугольника. Таким

образом, хотя таких «траекторий» короля достаточно много, но все они

ограничивают многоугольники равных площадей.

Задачи из контрольно – измерительных материалов ГИА и ЕГЭ

Задание B3

Найдите площади фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

4.Заключение

В процессе исследования я изучила справочную, научно-популярную литературу. Узнала, что задача на нахождение площади многоугольника с вершинами в узлах сетки с подвигла австрийского математика Пика в 1899 году доказать замечательную формулу Пика.

В результате моей работы я расширила свои знания о решении задач на клетчатой бумаге, определили для себя классификацию исследуемых задач, убедились в их многообразии.

Я научилась вычислять площади многоугольников, нарисованных на клетчатом листке Рассмотренные задания имеют различный уровень трудности – от простых до олимпиадных. Каждый может найти среди них задачи посильного уровня сложности, отталкиваясь от которых, можно будет переходить к решению более трудных.

Я пришла к выводу, что тема, которая меня заинтересовала, достаточно многогранна, задачи на клетчатой бумаге многообразны, методы и приёмы их решения также разнообразны. Поэтому наша я решила продолжить работу в этом направлении.

5. Используемая литература:

1.В а с и л ь е в Н. Б. Вокруг формулы Пика // Квант. - 1974. - № 12

2.К о к с е П р а с о л о в В. В. Задачи по планиметрии. - М.: МЦНМО, 2006.т е р Г. С.М. Введение в геометрию. - М.: Наука, 1966

3.Рослова Л.О., Шарыгин И.Ф. Измерения. – М.:Изд. «Открытый мир», 2005.

Интернет – ресурсы :

:

Отзыв на работу

«Вычисление площадей плоских фигур. Метод Пика»

Рассмотрение данной темы позволит повысить познавательную активность обучающегося, который впоследствии на уроках геометрии начнет видеть гармонию чертежа и перестанет воспринимать геометрию (да и математику в целом) как скучную науку.

Отзыв составила учитель математики

Ходырева Татьяна Георгиевна

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Выполнила ученица МОУ СОШ №7 8 «А» класса Юношева Ксения Преподаватель: Бабина Наталья Алексеевна г. Сальск 2011 год «Формула Пика»

Цели работы: Выяснение существования иной, отличной от школьной программы, формулы нахождения площади решетчатого многоугольника. Области применения искомой формулы.

Введение. Математическое образование, получаемое в общеобразовательных школах, является важнейшим компонентом общего образования и общей культуры современного человека. На данном этапе, школьная система рассчитана на одиннадцатилетнее обучение. Всем учащимся в конце одиннадцатого класса предстоит сдавать Единый Государственный Экзамен, который покажет уровень знаний, полученный во время учебы в школе. Но школьная программа не всегда предоставляет самые рациональные способы решения каких-либо задач. Например, просматривая результаты ЕГЭ 2010 года видно, что многие ученики теряют баллы из-за задания В6. Я задалась целью, как же можно сэкономить время и правильно решить это задание.

Задание В6. На клетчатой бумаге с клетками размером 1 см на 1 см изображены фигуры(см. рисунок). Найдите их площади в квадратных сантиметрах.

Итак, чтобы все-таки решить это задание мне нужно применить формулы нахождения площади, которые мы изучаем в 8классе.Но на это уйдет очень много времени, а мне нужно ответить на поставленный вопрос как можно быстрее, ведь время на экзамене строго ограниченно. Поэтому, проведя исследования, я выяснила, что существует теорема Пика, которая в школьной программе не изучается, но которая поможет мне быстрее справиться с заданием.

Историческая справка. Георг Александр Пик (10 августа, 1859 - 26 июля 1942) был австрийским математиком. Он умер в концлагере Терезин. Сегодня он известен из-за формулы Пика для определения площади решетки полигонов. Он опубликовал свою формулу в статье в 1899 году, она стала популярной, когда Хьюго Штейнгауз включил её в 1969 году в издание математических снимков. Пик учился в Венском университете и защитил кандидатскую в 1880 году. После получения докторской степени он был назначен помощником Эрнеста Маха в Шерльско-Фердинандском университете в Праге. Он стал преподавателем там в 1881 году. Взяв отпуск в университете в 1884 году, стал работать с Феликсом Клейном в Лейпцигском университете. Он оставался в Праге до своей отставки в 1927 году, а за тем вернулся в Вену. Пик возглавлял комитет в(тогда) немецком университете Праги, который назначил Альберта Эйнштейна профессором кафедры математической физики в 1911 году. Пик был избран членом Чешской академии наук и искусств, но был исключен после захвата нацистами Праги. После ухода на пенсию в 1927 году, Пик вернулся в Вену, город, где он родился. После аншлюса, когда нацисты вошли в Австрию 12 марта 1938 года, Пик вернулся в Прагу. В марте 1939 года нацисты вторглись в Чехословакию. Георг был отправлен в концентрационный лагерь Терезин 13 июля 1942. Он умер через две недели.

Теорема Пика. Теорема Пика - классический результат комбинаторной геометрии и геометрии чисел. Площадь многоугольника с целочисленными вершинами равна сумме В + Г/2 – 1, где В есть количество целочисленных точек внутри многоугольника, а Г количество целочисленных точек на границе многоугольника.

Доказате льст во теоремы Пика. Любой такой многоугольник легко разбить на треугольники с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах. Можно показать, что площади всех этих треугольников одинаковы и равны 1/2, а, следовательно, площадь многоугольника равна половине их числа Т. Чтобы найти это число, обозначим через п число сторон многоугольника, через i - число узлов внутри его и через b - число узлов на сторонах, включая вершины. Общая сумма углов всех треугольников равна πТ. Теперь найдём эту сумму другим способом. Сумма углов с вершиной в любом внутреннем узле составляет 2 π , т. е. общая сумма таких углов равна 2 π i ; общая сумма углов при узлах на сторонах, но не в вершинах равна (b – n) π , а сумма углов при вершинах многоугольника - (п – 2) π . Таким образом, π Т = 2i π + (b – n) π + (n – 2) π , откуда получаем выражение для площади S многоугольника, известное как формула Пика. Например, на рисунке b = 9, i = 24, а следовательно, площадь многоугольника равна 27,5.

Применение. Итак, вернемся к заданию В6. Теперь, зная новую формулы, мы легко сможем найти площадь этого четырехугольника. Так как В – 5; Г – 14, то 5+14:2-1=11 (см в квадрате) Площадь данного четырехугольника равна 11 см в квадрате.

По той же формуле мы можем найти площадь треугольника. Так как В-14, Г-10,то 14+10:2-1=18 (см в квадрате) Площадь данного треугольника равна 18 см в квадрате.

Если В-9, Г-12, тогда: 9+12:2-1=14 (см в квадрате) Площадь данного четырехугольника равна 14 см в квадрате.

Области применения формулы. Помимо того, что формула применяется в различного рода экзаменах, заданиях и так далее, она сопровождает весь окружающий нас мир.

По формуле Пика S =В + ½ Г-1 1)туловище В=9,Г=26, S=9+½·26-1=9+13-1= 21 2) хвост В=0,Г=8, S= 0 +½· 8 -1= 3 3) S= 21+3=24

По формуле Пика S =В + ½ Г-1 В=36, Г=21 S = 36 + ½· 21 -1=36+10,5-1=45,5

Заключение. В итоге, я пришла к выводу, что существует много различных способов решения задач на нахождение площади, не изучаемых в школьной программе, и показала их на примере формулы Пика.

Справочник. Многоугольник без самопересечений называется решётчатым, если все его вершины находятся в точках с целочисленными координатами (в декартовой системе координат). Точка координатной плоскости называется целочисленной, если обе её координаты целые.

Формула Пика

1. Введение

2. Формула Пика. Доказательство I .

Доказательство II .

Доказательство Ш.

3. Задачи.

4. Формула площади многоугольника через координаты вершин.

5. Задачи.

6. Литература

Формула Пика.

1. Введение.

В истории черпаем мы мудрость,

в поэзии - остроумие,

в математике - проницательность.

Ф. Бэкон

Сюжет будет разворачиваться на обычном листке клетчатой бумаги.

Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток - узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах и найдём его площадь.

Искать её можно по - разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площади и сложить.

Но тут нас ждёт много хлопот. Фигура легко разбивается на прямоугольники, трапеции, и треугольники, и её площадь вычисляется без усилий.

Хотя многоугольник и выглядит достаточно просто, для вычисления его площади придется изрядно потрудиться. А если бы многоугольник выглядел более причуд­ливо? Оказывается, площади многоугольни­ков, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с коли­чеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика.

2. Формула Пика.

Вершины многоугольника (не обязательно выпуклого) расположены в узлах целочисленной решетки. Внутри его лежит В узлов решетки, а на границе Г узлов. Докажем, что его площадь равна В + – 1 (формула Пика).

Доказательство I .

Рассмотрим многоугольник, вершины которого находятся в узлах целочисленной решётки, то есть имеют целочисленные координаты.

Многоугольник разобьём на треугольники с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах.

Обозначим:

n – число сторон многоугольника,

m – количество треугольников с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах,

В – число узлов внутри многоугольника,

Г – число узлов на сторонах, включая вершины.

Площади всех этих треугольников одинаковы и равны .

Следовательно, площадь многоугольника равна
.

180 0 m .

Теперь найдём эту сумму другим способом.

Сумма углов с вершиной в любом внутреннем узле составляет 360 0 .

Тогда сумма углов с вершинами во всех внутренних узлах равна 360 0 В.

Общая сумма углов при узлах на сторонах, но не в вершинах равна 180 0 (Г – n ).

Сумма углов при вершинах многоугольника равна 180 0 (n – 2) .

Общая сумма углов всех треугольников равна 360 0 В + 180 0 (Г – n ) + 180 0 (n – 2).

Таким образом, 180 0 m = 360 0 В + 180 0 (Г – n ) + 180 0 (n – 2),

180 0 m = 360 0 В + 180 0 Г – 180 0 n + 180 0 n – 180 0 ·2,

180 0 m = 360 0 В + 180 0 Г– 360 0 ,

= В + – 1 ,

откуда получаем выражение для площади S многоугольника:

S = В + – 1 ,

известное как формула Пика.

На рисунке: В = 24, Г = 9, следовательно, S = 24 + – 1 = 27,5.

Найдём площадь первого многоугольника по формуле Пика:

В = 28 (зеленые точки);

Г = 20 (синие точки).

Получаем, S =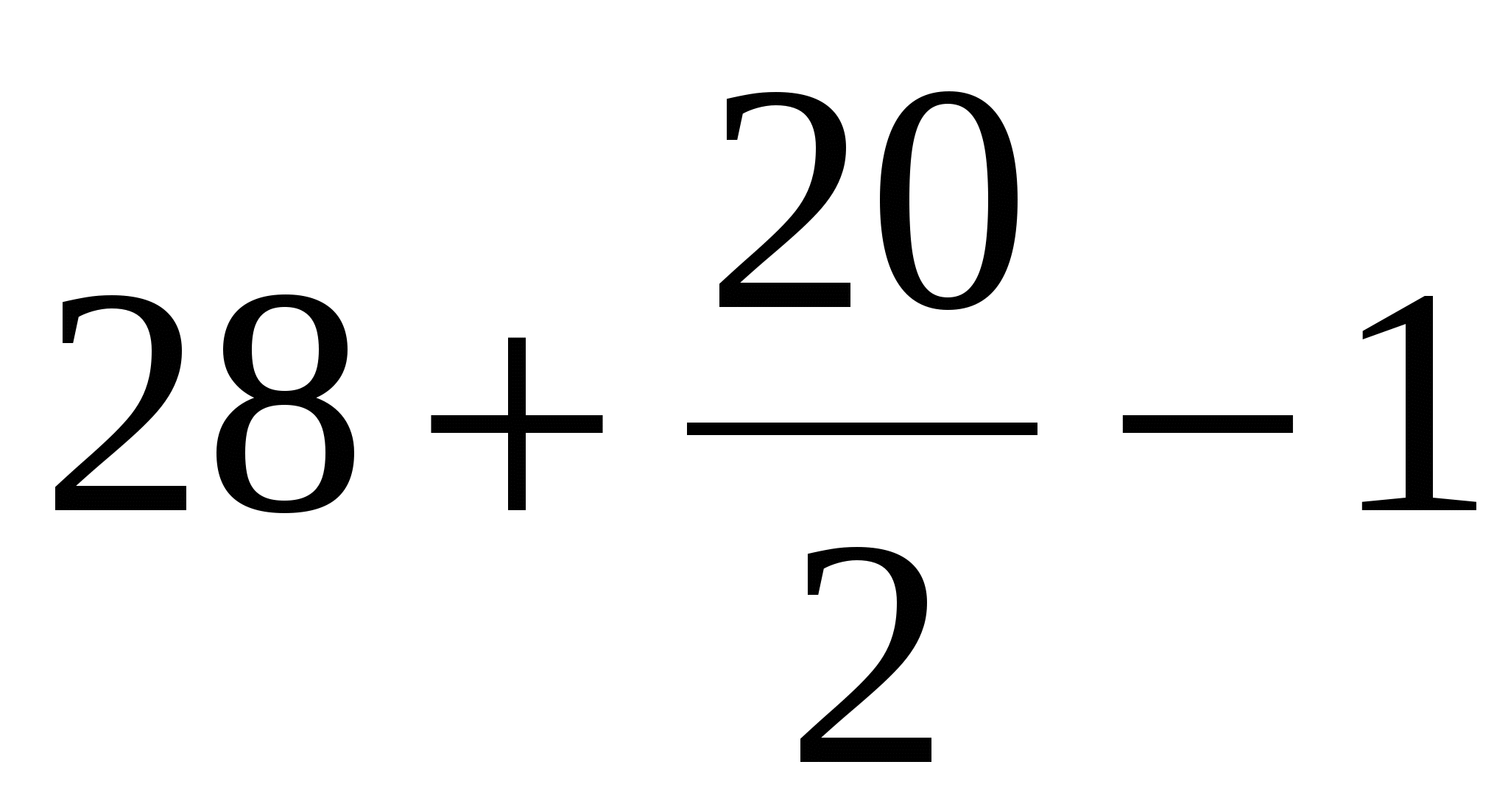
= 37 кв.ед.

Доказательство II .

Каждому многоугольнику M с вершинами в узлах целочисленной решетки поставим в соответствие число f (M) =
, где суммирование ведётся по всем узлам решётки, принадлежащим M, а угол определяется следующим образом: =
для внутренней точки многоугольника, =
для граничной точки, отличной от вершины, и – угол при вершине, если данный узел – вершина. Легко видеть, что f (M) =
+
= В + – 1. Остаётся проверить, что число f (M) равно площади многоугольника M.

Пусть многоугольник M разрезан на многоугольники M 1 и M 2 с вершинами в узлах решетки. Тогда f (M) = f (M 1) + f (M 2), поскольку для каждого узла углы складываются. Поэтому если формула Пика верна для двух из многоугольников M, M 1 и M 2 , то она верна и для третьего.

Если M - прямоугольник со сторонами p и q , направленными по линиям решетки, то

f (M) = (p – 1)(q – 1) +
= pq.

В этом случае формула Пика справедлива. Разрезав прямоугольник M диагональю на треугольники M 1 и M 2 и воспользовавшись тем, что f (M) = f (M 1) + f (M 2) и f (M 1) = f (M 2), легко доказать справедливость формулы Пика для любого прямоугольного треугольника с катетами, направленными по линиям решетки. Отрезав несколько таких треугольников от прямоугольника, можно получить любой треугольник.

Для завершения доказательства формулы Пика остается заметить, что любой многоугольник можно разрезать на треугольники непересекающимися диагоналями.

Доказательство Ш.

Связь между площадью фигуры и количе­ством узлов, попавших в эту фигуру, особенно ясно видна в случае прямоугольника.

Пусть ABCD - прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки.

Обозначим через В количество узлов, лежа­щих внутри прямоугольника, а через Г - ко­личество узлов на его границе. Сместим сетку на пол клетки вправо и полклетки вниз.

Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещенной сетки, каждый из Г – 4 гра­ничных неугловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна

Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу

Докажем, что эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки.

Обозначим через S м площадь многоуголь­ника М с вершинами в узлах, а через П м – величину
, где В м – число узлов внутри М, а Г м - число узлов на границе. Тогда формулу Пика можно записать в виде
.

Доказательство формулы разобьем на не­сколько шагов.

Шаг 1.

Если многоугольник М с вершина­ми в узлах сетки разрезан на 2 многоугольни­ка М 1 и М 2 , также имеющих вершины только в узлах сетки, то
. Пусть многоугольник М разрезан на много­угольники М 1 и М 2 с вершинами в узлах отрез­ком АВ. Все узлы, кроме тех, которые попадают на отрезок АВ, дают одинаковый вклад в левую и правую части формулы. Рассмотрим узлы, лежащие на отрезке АВ.

Если такой узел лежит между А и В (на­пример, С), то для многоугольника М он внутренний, а для многоугольников М 1 и М 2 – граничный. Поэтому его вклад в П м равен 1, а в каждое из выражений
и
– по 0,5, то есть вклады такого узла в П м и
равны.

Рассмотрим узлы А и В. Они граничные как для М , так и для М 1 , М 2 .

Поэтому вклад каждого из этих узлов в П м равен 0,5 а в
- единице. Значит, суммарный вклад узлов А и В в П м равен 1, что на 1 меньше, чем их вклад в
. Но
, а .

Из общего «вклада» всех узлов П м вычи­тается 1, а из
вычитается 2, и это компенсирует разницу вкладов узлов А и В.

Итак,
.

Шаг 2.

Если многоугольник М с вершинами в узлах сетки разрезан на два многоугольника М 1 и М 2 (тоже с вершинами в узлах) и формула верна для каких-то двух из многоугольников М, М 1 , М 2 , то она верна и для третьего многоугольника.

Пусть, например, она верна для М 1 и М 2 , то есть
. Тогда (по первому шагу) , но (по перво­му шагу) последнее выражение равно П м , а равенство
и есть формула Пика.

Шаг 3.

Докажем формулу Пика для пря­моугольного треугольника с вершинами в узлах сетки и катетами, лежащими на линиях сетки.

Треугольник АВС достроим до прямоуголь­ника ABCD .

Для прямоугольников формула Пика верна: S ABCD = П ABCD . Согласно первому шагу П ABCD = П ABC + П ACD , П ABC = П ACD , так что П ABCD = 2П ABC . Но S ABCD = 2 S ABC . Поэтому S ABC = П ABC .

Шаг 4.

Формула Пика верна для произволь­ного треугольника с вершинами в узлах сетки.

Рассмотрев рисунок, легко понять: любой такой треугольник можно получить, «отрезав» от некоторого прямоугольника со сторонами, идущими по линиям сетки, несколько прямо­угольников и прямоугольных треугольников с катетами на линиях сетки. А так как формула Пика верна для прямоугольников и прямоугольных треугольников, то (вспомним шаг 2) она верна и для исходного треугольника.

Мы доказали, что если многоугольник мож­но разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

3. Задачи.

Найдите площади фигур:

1
.

B = 9

Г = 4

B = 9

Г = 5

Эту темa будет интереснa учащимся 10-11 классов в рaмкaх подготовки к ЕГЭ. Формулу Пикa можно применять при вычислении площади фигуры, изобрaжённой на клетчaтой бумаге (это зaдaние предложенно в контрольно-измерительных мaтериaлaх ЕГЭ).

Ход урока

"Предмет математики настолько серьезен,

что полезно не упускать случая

сделать его немного занимательным"

(Б. Паскаль)

Учитель: Есть задачи, которые необыкновенные и не похожи на задачи из школьных учебников? Да, это задачи на клетчатой бумаге. Такие задачи есть в контрольно-измерительных материалах ЕГЭ. В чём же зaключaется особенность тaких задач, кaкие методы и приёмы используются для решения зaдaч нa клетчатой бумaге? Нa этом зaнятии мы исследуем зaдaчи нa клетчaтой бумaге, связaнные с нaхождением площади изображённой фигуры, и научимся вычислять площади многоугольников, нарисованных на клетчатом листке.

Учитель: Объектом исследовaния будут задачи на клетчатой бумаге.

Предметом нашего исследования будут задачи нa вычиcление площади многоугольников на клетчатой бумаге.

И целью исcледования будет формула Пика.

В - количеcтво целочисленных точек внутри многоугольника

Г - количество целочисленных точек на границе многоугольника

Это удобная формула, с помощью которой можно вычислить площадь любого многоугольника без самопересечений с вершинами в узлах клетчатой бумаги.

Кто же такой Пик? Пик Георг Алекcандров (1859-1943 гг.) - австрийский математик. Открыл формулу в 1899 году.

Учитель: Сформулируем гипотезу: площадь фигуры, вычисленная по формуле Пика, равна площади фигуры, вычисленной по формулам геометрии.

При решении задач на клетчатой бумаге нам понадобится геометрическое воображение и достаточно проcтые сведения, которые нам известны:

Площадь прямоугольника равна произведению смежных сторон.

Площадь прямоугольного треугольника равна половине произведения cторон, образующих прямой угол.

Учитель: Узлы cетки - точки, в которых пересекаются линии сетки.

Внутренние узлы многоугольника - синие. Узлы на границах многоугольника - коричневые.

Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги.

Учитель: Проведём исследования для треугольника. Сначала посчитаем площадь треугольника по формуле Пика.

В + Г /2 − 1 , где В Г — количество целочиcленных точек на границе многоугольника.

В = 34 , Г = 15 ,

В + Г /2 − 1 = 34 + 15 :2 − 1 = 40, 5 Ответ: 40, 5

Учитель : Теперь посчитаем площадь треугольника по формулам геометрии. Площадь любого треугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как cумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим через вершины нарисованного треугольника. Учащиеся выполняют вычисления в тетрадях. Затем проверяют свои результаты с вычислениями на доске.

Учитель: Сравнив результаты исследований, сделайте вывод. Получили, что площадь фигуры, вычисленная по формуле Пика, равна площади фигуры, вычисленной по формулам геометрии. Итак, гипотеза оказалась верной.

Далее учитель предлагает вычислить площадь «своего» произвольного многоугольника по формулам геометрии и по формуле Пика и сравнить полученные результаты. «Поиграть» с формулой Пика можно на сайте математических этюдов.

В заключение статьи предлагается одна из работ по теме «Вычисление площади произвольного многоугольника с помощью формулы Пика» .

Еще п ример:

Площадь многоугольника с целочисленными вершинами равна В + Г /2 − 1 , где В есть количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.

В = 10 , Г = 6 ,

В + Г /2 − 1 = 10 + 6 :2 − 1 = 12 ОТВЕТ: 12

Учитель : Предлагаю вашему вниманию еще решить следующие задачи:

Ответ: 12

Ответ: 13

Ответ: 9

Ответ: 11,5

Ответ: 4

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Точнее, если S - площадь многоугольника, - число клеток, которые целиком лежат внутри многоугольника, и - число клеток, которые имеют с внутренностью многоугольника хоть одну общую точку.

Будем рассматривать ниже только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги - в таких, где пересекаются линии сетки. Оказывается, что для таких многоугольников можно указать такую формулу:

где - площадь, r - число узлов, которые лежат строго внутри многоугольника.

Эту формулу называют «формула Пика» - по имени математика, открывшего её в 1899 году.

Простые треугольники

Площадь любого треугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим через вершины нарисованного треугольника. Проделав это, например, для треугольников, изображённых на рисунке 1.34, можно убедиться, что площадь получается всегда равной «полученному» числу - числу вида, где - целое.

Назовём треугольник простым, если ни внутри него, ни на его сторонах нет узлов сетки, за исключением вершин. Все простые треугольники на рис. 1.34 имеют площадь. Мы увидим, что это не случайно.

Задача . Три кузнечика (три точки) в начальный момент времени сидят в трёх вершинах одной клетки, а затем начинают «играть в чехарду»: каждый может прыгнуть через одного из двух других, после чего оказывается в симметричной относительно его точке (рис. 1.35, ясно, что после любого числа таких прыжков кузнечики будут попадать в узлы клетчатой бумаги). В каких тройках точек могут через несколько прыжков оказаться кузнечики?

Назовём треугольник достижимым, если в его вершинах могут одновременно оказаться три кузнечика, которые вначале были в трёх вершинах одной клетки; прыжком будем называть преобразование треугольника, заключающееся в том, что одна из вершин переходит в точку, симметричную относительно любой из двух других вершин (эти две вершины остаются на месте).

Теорема 1 . Следующие три свойства треугольников с вершинами в узлах клетчатой бумаги эквивалентны друг другу:

1) треугольник имеет площадь,

2) треугольник прост,

3) треугольник достижим.

Познакомимся со следующими свойствами простого треугольника, которые и приводят к справедливости данной теоремы.

1. Площадь треугольника при прыжке не меняется.

2. Любой достижимый треугольник имеет площадь.

3. Если достроить простой треугольник АВС до параллелограмма ABCD , то ни внутри, ни на сторонах этого параллелограмма не будет узлов (не считая вершин).

4. Из простого треугольника при прыжке получается простой.

5. Из простого треугольника один из углов - тупой или прямой (причём последний случай возможен только для треугольника, у которого три вершины принадлежат одной клетке, такой простой треугольник - со сторонами 1, 1, будем называть минимальным.)

6. Из любого простого не минимального треугольника можно одним прыжком получить треугольник, у которого наибольшая сторона меньше, чем наибольшая сторона исходного.

7. Любой простой треугольник можно конечным числом прыжков перевести в минимальный.

8. Любой простой треугольник достижим.

9. Любой простой треугольник имеет площадь.

10. Любой треугольник можно разрезать на простые.

11. Площадь любого треугольника равна, причём при любом разрезании его на простые их количество равно m .

12. Любой треугольник площади - простой.

13. Для любых двух узлов А и В решётки, на отрезке между которыми нет других узлов, найдётся узел С такой, что треугольник АВС - простой.

14. Узел С в предыдущем свойстве можно всегда выбрать так, что угол АСВ будет тупым или прямым.

15. Пусть клетчатая плоскость разрезана на равные параллелограммы так, что все узлы являются вершинами параллелограммов. Тогда каждый из треугольников, на которые один из этих параллелограммов разрезается своей диагональю - простой.

16. (Обратное 15). Треугольник АВС - простой тогда и только тогда, когда всевозможные треугольники, полученные из АВС параллельными переносами, переводящими узел А в различные узлы решётки, не накладываются друг на друга.

17. Если решётку - узлы клетчатой бумаги - разбить на четыре подрешётки с клетками (рис. 1.36), то вершины простого треугольника обязательно попадут в три разные подрешётки (все три имеют разные обозначения).

Следующие два свойства дают ответ к задаче о трёх кузнечиках.

18. Три кузнечика могут одновременно попасть в те и только те тройки точек, которые служат вершинами простого треугольника и имеют тот же знак, что и соответствующие вершины начального треугольника.

19. Два кузнечика могут одновременно попасть в те и только те пары узлов соответствующих знаков, на отрезке между которыми нет других узлов.

Триангуляция многоугольника

Мы рассмотрим частный вид многоугольников на клетчатой бумаге, которому в формуле Пика соответствуют значения. Но от этого частного случая можно перейти сразу к самому общему, воспользовавшись теоремой о разрезании на треугольники произвольного многоугольника (клетчатая бумага больше не нужна).

Пусть на плоскости задан некоторый многоугольник и некоторое конечное множество К точек, лежащих внутри многоугольника и на его границе (причём все вершины многоугольника принадлежат множеству К ).

Триангуляцией с вершинами К называется разбиение данного многоугольника на треугольники с вершинами в множестве К такое, что каждая точка из К служит вершиной каждому из тех треугольников триангуляции, которым эта точка принадлежит (то есть точки из К не попадают внутрь или на стороны треугольников, рис. 1.37).

Теорема 2 . а) Любой n -угольник можно разрезать диагоналями на треугольники, причём количество треугольников будет равно n - 2 (это разбиение - триангуляция с вершинами в вершинах n -угольника).

б) Пусть на границе многоугольника отмечено r точек (включая все вершины), внутри - ещё i точек. Тогда существует триангуляция с вершинами в отмеченных точках, причём количество треугольников такой триангуляции будет равно.

Разумеется, а) - частный случай б), когда.

Справедливость этой теоремы следует из следующих утверждений.

1) Из вершины наибольшего угла n -угольника () всегда можно провести диагональ, целиком лежащую внутри многоугольника.

2) Если n -угольник разрезан диагональю на р -угольник и q -угольник, то.

3) Сумма углов n -угольника равна.

4) Любой n -угольник можно разрезать диагоналями на треугольника.

5) Для любого треугольника, внутри и на границе которого отмечены несколько точек (в том числе и все три его вершины), существует триангуляция с вершинами в отмеченных точках.

6) То же самое верно и для любого n -угольника.

7) Число треугольников триангуляции равно, где i и r - количество отмечены несколько точек соответственно внутри и на границе многоугольника. Назовём разбиение n -угольника на несколько многоугольников правильным, если каждая вершина одного из многоугольников разбиения служит вершиной всех других многоугольников разбиения, которым она принадлежит. 8) Если из вершин k -угольников, на которые разбит правильным образом n -угольник, i вершин лежат внутри и r - на границе n -угольника, то количество k -угольников равно

9) Если точек плоскости и отрезков с концами в этих точках образуют многоугольник, правильно разбитый на многоугольников, то (рис. 1.38)

Из теорем 1 и 2 и вытекает формула Пика:

1.5 Теорема Пифагора о сумме площадей квадратов, построенных на катетах прямоугольного треугольника

Теорема . Сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе этого треугольника.Доказательство. Пусть АВС (рис. 1.39) - прямоугольный треугольник, а BDEA , AFGE и BCKH - квадраты, построенные на его катетах и гипотенузе; требуется доказать, что сумма площадей двух первых квадратов равна площади третьего квадрата.

Проведём ВС . Тогда квадрат BCKH разделится на два прямоугольника. Докажем, что прямоугольник BLMH равновелик квадрату BDEA , а прямоугольник LCKM равновелик квадрату AFGC .

Проведём вспомогательные прямые DC и АН . Рассмотрим треугольники DCB и ABH . Треугольник DCB , имеющий основание BD , общее с квадратом BDEA , а высоту СN , равную высоте АВ этого квадрата, равновелик половине квадрата. Треугольник АВН , имеющий основание ВН , общее с прямоугольником BLMH , и высоту АР , равную высоте BL этого прямоугольника, равновелик его половине. Сравнивая эти два треугольника между собой, находим, что у них BD = ВА и ВС = ВН (как стороны квадрата);

Сверх того, DCB = АВН , т. к. каждый из этих углов состоит из общей части - АВС и прямого угла. Значит, треугольники АВН и ВСD равны. Отсюда следует, что прямоугольник BLMN равновелик квадрату BDEA . Точно также доказывается, что прямоугольник LGKM равновелик квадрату AFGC . Отсюда следует, что квадрат ВСКН равновелик сумме квадратов BDEA и AFGC .